ブログ
2020年 10月 16日 【力学】2質点系の運動その2
皆さんこんにちは。
担任助手1年の中村祐貴です。
進捗いかがでしょうか。
さて,前回お届けした【力学】2質点系の運動その1取り組んでいただけましたでしょうか。
まだの方はそちらを先にどうぞ。
前回扱った弾性衝突の反発係数(はねかえり係数)が
1であることの意味について,少し考えてみましょう。
まず,反発係数の定義は何でしたでしょうか。
そうですね。
衝突前後の相対速さの比ですね。
すなわち,衝突直前の物体1及び物体2の速度が![]() ,
,
衝突直後の速度が![]() とすると,
とすると,
衝突直前の物体1から見た物体2の相対速度![]() および
および
衝突直後の物体1から見た物体2の相対速度![]() は,
は,
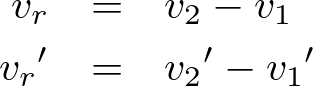
で表されるので,
衝突前後で![]() と
と![]() の相対速度の符号は明らかに逆転する
の相対速度の符号は明らかに逆転する
(自分の視点で考えると自分に対して突っ込んできたやつは
衝突したら逆方向に飛んでいく)ため,
反発係数![]() は次のように定義できます。
は次のように定義できます。
![\begin{eqnarray*}
e=\textcolor[rgb]{1,0.4,0.4}{-}\frac{{v_r}'}{v_r}=\textcolor[rgb]{1,0.4,0.4}{-}\frac{{v_2}'-{v_1}'}{v_2-v_1}
\end{eqnarray*}](https://texclip.marutank.net/render.php/texclip20201013210621.png?s=%5Cbegin%7Beqnarray*%7D%0Ae%3D%5Ctextcolor%5Brgb%5D%7B1%2C0.4%2C0.4%7D%7B-%7D%5Cfrac%7B%7Bv_r%7D%27%7D%7Bv_r%7D%3D%5Ctextcolor%5Brgb%5D%7B1%2C0.4%2C0.4%7D%7B-%7D%5Cfrac%7B%7Bv_2%7D%27-%7Bv_1%7D%27%7D%7Bv_2-v_1%7D%0A%5Cend%7Beqnarray*%7D&f=c&r=300&m=p&b=f&k=f)
ここまでみてわかるように,
反発係数が1であるとは相対速さが不変で
相対速度の符号のみが変化するということです。
これは非常に重要なことなので,
しっかりと頭に入れておいてください。
ところで,この相対速度は少し別な見方をすることで
より深い考察が得られます。
それは,重心を基準に考えることです。
そもそも重心とは何だったでしょうか?
ここで2質点の運動方程式を考えてみましょう。
運動方程式は,
%5C%5C%0Am_2a_2%26%3D%26F_%7B2%2C1%7D%20-%20F_%7B2%2Cex%7D~~~~%5Ccdot%5Ccdot%5Ccdot(2)%0A%5Cend%7Beqnarray*%7D&f=c&r=300&m=p&b=f&k=f)
となります。
ここに,![]() は物体1が物体2から受ける内力,
は物体1が物体2から受ける内力,
同様に![]() は物体2が物体1から受ける内力で
は物体2が物体1から受ける内力で
これらは作用・反作用の関係にあります。
また,![]() や
や![]() はそれぞれ物体1や物体2が
はそれぞれ物体1や物体2が
系の外から受ける外力(external force)です。
おそらく,皆さんの多くは,でどうすんの?
と思われていることでしょう。
そもそも衝突時の内力は特に撃力とよばれる
非常に大きな力ですから,これを求めるのは難しいです。
そこで![]() と
と![]() が作用・反作用の関係にあることを考えると,
が作用・反作用の関係にあることを考えると,
![]()
が成立しているわけですから,
先ほどの2式をどうしたらよさそうですか??
そうですね。
![]()
となるのですから,辺々足すのがよさそうですね。
(1)+(2)により,
%0A%5Cend%7Beqnarray*%7D&f=c&r=300&m=p&b=f&k=f)
が得られます。このままでもよいのですが,
(1)+(2)=(3)は2つの物体を1つのセットとみなして
連立方程式を立てたことに相当するので,
そのことがより伝わる表式に直してみましょう。
すなわち,![]() を用いて,
を用いて,
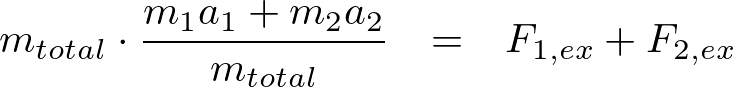
と書き表せるので,ここで重心Gの座標を
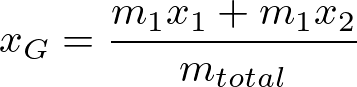
で定めると,重心加速度![]() が
が
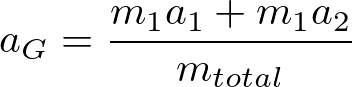
となりますから(3)式は結局,

と書き換えられるわけです。
これは何を意味しているのでしょうか。
そうですね。重心の運動は,それぞれの物体にかかる外力が
あたかもすべて重心1点にかかっていると考えたときの
運動に他ならないわけです。
なるほど。特に外力が0の時は,重心加速度は0,
すなわち重心速度不変ということなのです!!
超重要
え,でも待って?
これって運動量保存と同じじゃない?と思った方,
素晴らしいです。
その通りです。
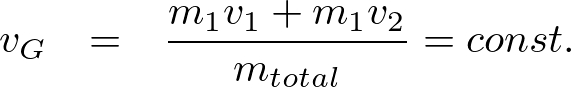
(const.はconstantの略で定数の意)なのですから,
![]()
と同じことですからね。(質量は勿論定数です!!)
運動量保存も実はこれと同様にして導かれるので,
重心速度一定か運動量保存かどちらの言葉を使っても構いません。
少し長くなってしまったので,
今回はここで区切りましょう。
続編は今回やったことをもとに
重心から見た相対速度の議論を深めます。
近日公開ということで。
質問はいつでも受け付けているので気軽にどうぞ。
さて,今月のブログは生きがいがテーマでしたが,
私のいまの生きがいは少しでも実力をつけて
将来社会により貢献できるようにすることですね。
施されたら施し返す。
恩返しです!(笑)
でも本当にこれからの社会を作っていくのは我々なので,
しっかりと精進してまいりましょう。
では,勉強頑張ってください。
横浜国立大学理工学部
担任助手1年 中村 祐貴
















