ブログ | 東進ハイスクール 青葉台校 大学受験の予備校・塾｜神奈川県 - Part 2

東進ハイスクール 青葉台校 » 2020年9月

ブログ　2020年09月の記事一覧

2020年 9月 24日　クスりが薬。　

こんにちは。

東京理科大学経営学部３年の大岩優斗です。

このブログがいつ投稿されるのか

全くわかりませんが、

きっと担任助手が受験生時代に

聞いていた曲や

支えになっていた名言を

テーマにブログを書いていると思います。

南雲さんサウジアラビアのことわざの話してましたね。

これ余談なんですけど、

大岩と南雲は同じ小学校に通っていました。

あとこれ余談なんですけど、

南雲さんは雑にいじればいじるほど輝きます。

 

さて、そろそろ本題に入ろうと思いますが、

今日、大岩が紹介するのは

「好きなやりとり」

好きなやきとり(ぼんじり)

ではなく、

好きなあやとり(ほうき)

でもなく、

好きなやりとり

です。

 

あまり音楽を聴かないのと、

支えになった名言が特に思い出せなかったので、

おおいわ好みのやりとりを

紹介します。

共感できた人は受付でその話しましょう。

今回のブログでは、手始めに1つご紹介します。

 

1.ボーダー論(ドラマ「カルテット」より)

服がボーダーかぶりした2人のやりとり。

 

「なんでボーダー着るかな？」

「ボーダー着ちゃダメなんですか？」

「絶対かぶるに決まってるじゃない。

着るとき、他にも誰か着てる人いるかな？

って普通考えません？」

「じゃあ、ボーダーはいつ着ればいいんですか？」

「昨日ボーダー着てる人と会うときじゃないですか。」

「ちょっと、条件が厳し過ぎません？笑」

 

はい。偏見まみれのこの言い草がなんとも面白い。

けっして、大笑いはしないけど、

なんかくすりと笑ってしまう、

そんなやりとりです。

おおいわはこんな会話が大好きなので、

ぜひおすすめがあれば紹介してほしいし、

実際にこういう会話したい人がいたら

ぜひしましょう。

あ、これ余談なんですけど、

南雲さんのiPhoneの言語設定

アラビア語です。

 

担任助手３年　大岩優斗

 

 

 

 

2020年 9月 23日　石油を掘れ。

皆さんこんにちは！

電気通信大学3年の南雲です。

 

突然ですが皆さん、

こんなことわざを

知っていますか。

 

‘石油が出るか出ないかは、

掘ってみなければわからない。

 

 

これはサウジアラビアの

ことわざです。

 

意味はわからないですが、

なんだか深い言葉ですよね。

 

それはさておき、今日は受験期に

聞いていた音楽について

書きたいと思います。

 

私は勉強中基本的に

音楽は聴いていませんでした。

 

おっと、1行目から

根も葉もないことを言ってしまった。

 

というのも、音楽は

集中できなかった時の最終兵器

みたいな感じで聴いていたので、

これといって印象に残るものが

ありません、、

 

強いて言えば、クラシックを

聴いていましたね。

個人的には

ドヴォルザークの「新世界より」

とか、

ショスタコーヴィチの交響曲第5番

とか、

激し目の曲を聞いていた気がします。

 

何言っているかわからないって？

時間がある時聞いてみてください。

アガります。

 

そんな私の新たな一面を

皆さんにお見せしたところで、

 

かの有名な作曲家、

ベートーヴェンの名言をここに記し、

締めくくりとさせていただきます。

 

‘苦難の時に動揺しないこと、

これが真に賞賛すべき人物の

証拠である。

 

皆さんもこれから

苦しい時が続くかもしれません。

そんな時、動揺せずに、

まずは落ち着いて周りを見て、

やるべきことを考えていきましょう。

 

そう、穴を掘って

石油が出なかったとしても、

そこに石油がなかったことが

わかったことは収穫です。

落ち着いて次の穴を

掘ればいいのです。

 

 

 

 

さて今回の数学クイズはこちら。

 

これからあるクラスに

生徒を集めます。

クラスの中に同じ誕生日の人が

2人以上いる確率が

50%以上になるには、

何人生徒を集めればいいでしょう？

※閏年、双子は考えないものとする。

 

 

①23人

②78人

③183人

④365人

 

 

 

 

皆さんわかりましたか？

これは相当難しいですね。

 

 

 

正解は、、

 

①の23人です！

 

 

意外に少ないですよね！！

クラスの中の誰でもいいから

同じ人がいればいい

とすると、こんなに少なくなるんです。

 

 

以下、難しい話するので、

数学使わない人は

へ〜〜

と思っておいてください(笑)

 

 

1年は365日なので、

誕生日は365通りでどの日に生まれる

確率も同様に確からしいとします。

 

「n人の中に同じ誕生日の人が

少なくとも2人いる確率」

 

を求めたいので、ここでは

余事象を考えます。

 

つまり、

1-(n人全員が違う誕生日である確率)

を計算すればいいのです。

 

「少なくとも〇〇」

というワードがヒントですね。

 

n人全員が違う誕生日である確率を

Pとすると、求める確率は

1-Pとなります。

 

二人目の誕生日が一人目と違う

確率は、364/365、

三人目の誕生日が一、二人目と違う

確率は、363/365、

n人目の誕生日が…確率は、

(365-n+1)/365

となります。

 

というように全てを

掛け合わせていくと、

 

P = 364•363•…•(365-n+1)/365^n

つまり、

P = 365!/(365^n)•(365-n)!

 

となります。

 

つまり求める確率は、

1-Pより、

1 – 365!/(365^n)•(365-n)!

 

このnに数字を代入していくと、

n = 22の時、0.47569…

n = 23の時、0.50829…

となり、

23人の時確率が

50%を超えるんですね。

 

いかがでしたか？

余事象で考えること、

数学使う人は要復習！

 

 

明日のブログもお楽しみに！

 

担任助手3年 南雲拓真

 

 

2020年 9月 22日　飲むものではない。観るものだ。　

こんにちは！担任助手２年の富浜です！

 

つい先日最終回を迎えたドラマ、MIU４０４の余韻に浸ってます。

受験生のみんなはドラマを見る暇はないと思うので、ぜひ受験を終えた後にTverに契約して観てみてください！

菅田将暉、かっこよすぎる。。。結婚したい。。。

 

そんな妄言はさておき

 

みなさん。元気ですか！！！！！！！！！！！

 

アントニオ猪木と申します(違います)

 

「元気があればなんでもできる」と言いますが、受験期はそうも行きませんよね。

元気がない時も多いと思います。

 

元気がなくて力が出ない・・・

バタ子さんがいれば新しい顔に変えてもらえるが、そんな人はおらん。そもそもそんなことできん。

 

じゃあどうする？どうやって元気100倍に戻るか。

 

ふざけるのはここまで笑

 

元気がない人間が取る行動は二つある！

 

①自分より頑張っている人、キラキラしているものをみて元気をもらう

②自分劣っているものに目を向けることで自己肯定感を高め、活力にする

 

どっちを取るかに不正解はない。が、富浜は①側の人間でした。

 

自分は②側の人だよーーーって人はここでブラウザバックして勉強に戻って構いません！

 

 

自分はどうしても元気がない時、キラキラしてるものを見て元気をもらってました。「キラキラ」っていうのは物理的ではなく、存在としてキラキラしているものです。

 

そのキラキラしてるものってのは人それぞれ。

自分の友達・先輩・アスリート・アイドル・アニメ・バンド、音楽？、ドラマ？

 

まぁなんでもいいんです。

 

 

本題はここから。僕のキラキラは何だったか。それは

 

ポカリスエットのCM

 

です。

 

ぜひyoutubeで検索して観てほしい。

 

大量の高校生が制服とか部活着で踊って歌ってるんです。

ダンス揃ってるし、楽しそうだし、歌もいい。団結力とかそういうものがひしひしと伝わってくる。

 

まじで青春。キラッキラ。

 

めちゃくちゃ元気でます。

 

僕にとってポカリスエットは飲むものではないんです。観るものなんです。

 

ここでタイトルを回収していく。

 

 

でもこれを読んで「は？なに言ってんの？元気なんか出ねーよ」って思った人いませんか？

 

そんな人は僕に相談しに来てください。全部話聞きます！

 

必ず力になるので、ぜひ頼ってください。

 

一緒に頑張ろう！

担任助手２年　富浜大護

 

 

 

 

 

 

 

 

 

 

 

 

2020年 9月 21日　【力学】２質点系の運動その１

皆さんこんにちは。

横浜国立大学理工学部，担任助手1年の中村祐貴です。

皆さん進捗いかがですか？

最近は過去問演習や単元ジャンル別演習にいそしんでいることと思いますが，
最近ある生徒の答案を見て少し気になったので今回このテーマを扱います。
（皆さんが出している答案は私が受け取った時は軽く見させていただいてます笑）

今回の内容は全員が必ず押さえなければならない”must”の内容ですが，
続編（その２）はやや発展的な内容とはいえ，
知っていると物理的内容の見通しが良くなると思われるので，頑張っていきましょう。
（ただ難関大や物理系に進もうと考えている人にとっては続編も含めshould ~ mustです！）

今回の設定は以下の通りです。
とはいっても，非常に典型的なお話ですが。

質量m1, m2の２質点が右向きを正とした速度v1, v2で弾性衝突し，
その直後のそれぞれの速度v1‘, v2‘を求めていきましょう。

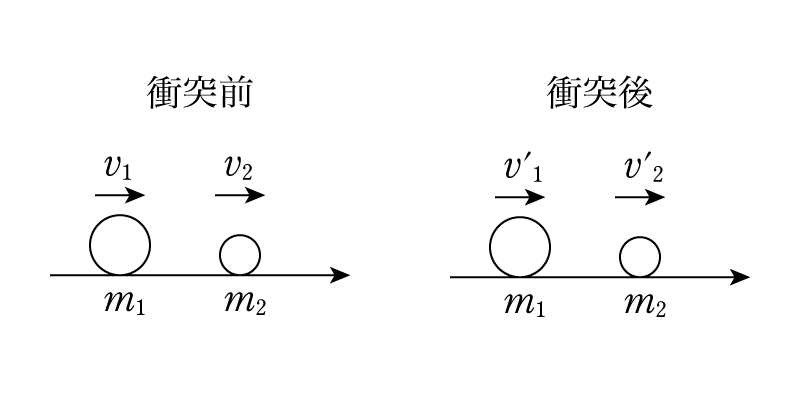画像引用：https://physics-school.com/two-body-energy/

 問題自体は具体的な値であれば共通試験レベルなので，
できてほしいのですが，いかがでしょうか。

 

もし，手詰まりになったとするならば次のようにやったのではないでしょうか。

想定解答①

内力のみがはたらくので，運動量保存則より，
\begin{eqnarray*} m_1v_1+m_2v_2=m_1v_1'+m_2v_2' \cdot\cdot\cdot(1) \end{eqnarray*}

また，力学的エネルギー保存則より，
\begin{eqnarray*} \frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1{v_1'}^2+\frac{1}{2}m_2{v_2'}^2 \cdot\cdot\cdot(2) \end{eqnarray*}

え？これを代入するのかって？

まあこの式を立ててしまったのなら，解くためには代入するしかないでしょうか…
一応その過程を以下に示します。

代入計算過程

(１)式をv2‘について解いて，

\begin{eqnarray*} v_2'=\frac{m_1}{m_2}(v_1-v_1')+v_2\cdot\cdot\cdot(1)' \end{eqnarray*}
これを(２)式に代入して両辺を２倍すると，
（v2‘を消去してv1‘についての解を得たい！）
\begin{eqnarray*} m_1v_1^2+m_2v_2^2=m_1{v_1'}^2+m_2\left(\frac{m_1}{m_2}(v_1-v_1')+v_2\right)^2 \end{eqnarray*}
\begin{eqnarray*} m_1v_1^2+\textcolor[rgb]{0.2,0.4,1}{m_2v_1^2}=m_1{v_1'}^2+\frac{m_1^2}{m_2}(v_1-v_1')^2+2m_1(v_1-v_1')v_2+\textcolor[rgb]{0.2,0.4,1}{m_2v_1^2} \end{eqnarray*}
（消えること自体は展開前から見えていてほしいが）
青い部分を両辺から引いて整理すると
\begin{eqnarray*} m_1v_1^2=m_1{v_1'}^2+\frac{m_1^2}{m_2}(v_1-v_1')^2+2m_1(v_1-v_1')v_2 \end{eqnarray*}
となり，両辺をm1で割って，
\begin{eqnarray*} v_1^2={v_1'}^2+\frac{m_1}{m_2}(v_1-v_1')^2+2(v_1-v_1')v_2 \end{eqnarray*}
をv1‘の２次方程式として整理すると，
\begin{eqnarray*} \left(1+\frac{m_1}{m_2}\right){v_1'}^2-2\left(\frac{m_1}{m_2}v_1+v_2\right)v_1'+2v_1v_2-\left(1-\frac{m_1}{m_2}\right)v_1^2=0 \end{eqnarray*}
\begin{eqnarray*} v_1'=\frac{\frac{m_1}{m_2}v_1+v_2\pm\sqrt{\left(\frac{m_1}{m_2}v_1+v_2\right)^2-\left(1+\frac{m_1}{m_2}\right)\left(2v_1v_2-\left(1-\frac{m_1}{m_2}\right)v_1^2\right)}}{1+\frac{m_1}{m_2}} \end{eqnarray*}
を得て，根号（ルート）の中身について項ごとに整理すると，
\begin{eqnarray*} &\ &\left(\frac{m_1}{m_2}v_1+v_2\right)^2-\textcolor[rgb]{0.2,0.4,1}{\left(1+\frac{m_1}{m_2}\right)}\left(2v_1v_2-\textcolor[rgb]{0.2,0.4,1}{\left(1-\frac{m_1}{m_2}\right)}v_1^2\right)\\ &=&\left(\frac{m_1}{m_2}v_1\right)^2+2\frac{m_1}{m_2}v_1v_2+v_2^2+\left(\textcolor[rgb]{0.2,0.4,1}{1-\left(\frac{m_1}{m_2}\right)^2}\right)v_1^2-2\left(1+\frac{m_1}{m_2}\right)v_1v_2\\ &=&v_1^2-2v_1v_2+v_2^2\\ &=&(v_1-v_2)^2 \end{eqnarray*}となるから，
\begin{eqnarray*} v_1'=\frac{\frac{m_1}{m_2}v_1+v_2\pm(v_1-v_2)}{1+\frac{m_1}{m_2}} \end{eqnarray*}
を得る。
ここで，この複号の+側はv1‘=v1という衝突直前の自明な関係が得られるだけなので，
－側を取ることで，求めるv1‘の解
\begin{eqnarray*} v_1'&=& \frac{\frac{m_1}{m_2}v_1+v_2-(v_1-v_2)}{1+\frac{m_1}{m_2}}\\ &=& \frac{\frac{m_1}{m_2}-1}{\frac{m_1}{m_2}+1}v_1+\frac{2}{\frac{m_1}{m_2}+1}v_2\\ &=& \frac{m_1-m_2}{m_1+m_2}v_1+\frac{2m_2}{m_1+m_2}v_2\\ \end{eqnarray*}
を得る。これを(１)’式に代入してv2‘の解
\begin{eqnarray*} v_2'&=&\frac{m_1}{m_2}\left(v_1-\left(\frac{m_1-m_2}{m_1+m_2}v_1+\frac{2m_2}{m_1+m_2}v_2\right)\right)+v_2\\ &=&\frac{m_1}{m_2}\left(\frac{2m_2}{m_1+m_2}v_1-\frac{2m_2}{m_1+m_2}v_2\right)+v_2\\ &=&\frac{2m_1}{m_1+m_2}v_1+\frac{m_2-m_1}{m_1+m_2}v_2 \end{eqnarray*}
を得る。

いやー，だるい！長い！


もちろんこの計算をこなす計算力は必要なので，
各自 上の記述を隠してできるかどうか確認してみてほしいですが，
これを試験中にやるのは賢明ではないでしょう。

ではどうするのか。

 


実は，数学的な対称性を用いれば比較的容易に解くことができます。

 想定解答①のつづき
(１)式及び(２)式は対称性に注意して次のように変形できる。
\begin{eqnarray*} \left\{ \begin{array}{llll} m_1(v_1-v_1')&=&m_2(v_2'-v_2)&\cdot\cdot\cdot(1)''\\ \frac{1}{2}m_1(v_1^2-{v_1'}^2)&=&\frac{1}{2}m_2({v_2'}^2-v_2^2)&\cdot\cdot\cdot(2)' \end{array} \right. \end{eqnarray*}
(１)”式の両辺は０でないので（０となるのは衝突前である！），
(２)’式を(１)”式で辺々割って両辺２倍することで，
\begin{eqnarray*} v_1+v_1'=v_2+v_2' \end{eqnarray*}
\begin{eqnarray*} v_2'=v_1-v_2+v_1' \end{eqnarray*}
となり，これと(１)’式とあわせて，
\begin{eqnarray*} v_2'=v_1-v_2+v_1'&=&\frac{m_1}{m_2}(v_1-v_1')+v_2\\ \therefore \left(1+\frac{m_1}{m_2}\right)v_1'&=&\left(\frac{m_1}{m_2}-1\right)v_1+2v_2\\ \therefore v_1'&=&\frac{\left(\frac{m_1}{m_2}-1\right)v_1+2v_2}{1+\frac{m_1}{m_2}} \end{eqnarray*}
（以下同様）

これならば計算量はさほど悪くはないですね。

一方，多くの「解けた」人は恐らく次のようにやったのではないでしょうか。

 想定解答②
(２)式の代わりに弾性衝突であることから反発係数は１ゆえ，
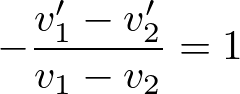
\begin{eqnarray*} -\frac{v_1'-v_2'}{v_1-v_2}=1 \end{eqnarray*}
を用いてこれを整理すると，
\begin{eqnarray*} v_2'=v_1-v_2+v_1' \end{eqnarray*}
（以下同様）
はい。こちらのほうが①より物理的な解答といえるでしょう。
ここまではこの記事を読んでくれた全員に抑えていただきたいmustの内容です。

しかし，これの「意味」がしっかりと分かっているならば，
より自然な解答を得ることができますが，
これを考えるのはみなさんの宿題とします。

続編で答え合わせをしましょう。


先に知りたい！という人は直接言ってくださればお答えします。

それでは，勉強頑張ってください。

担任助手１年　中村
 

 

 
 

2020年 9月 20日　あなたにこの言葉を贈ります。

夏休みが終わって暫く経ちましたね。

ところで、あなたは日々モチベーションを保てていますか？

勉強は大変だけれど達成感や成長を感じ、充実していると思える日々を送れているという人はvery good!そのまま突っ走れ！

でも、、

刻一刻と近づいてくる試験日。やらなければいけないからとやる気の出ない心に蓋をしていたりしませんか？

今だけは、そんな足を引っ張っている心と向き合ってみませんか？

自分の中のもやもやした気持ちは目を逸らすのではなくしっかり見て整理する方が楽なものです。

今回はそのお手伝いをしようと思い、皆さんと同じ高校生のゲストを３人呼びました！

では落込さん(3年生)、MaXさん(3年生)、楽観さん(2年生)よろしくお願いします

よろしくお願いします！

まずは落込さん。落込さんは高校３年生でしたよね？夏休みは充実した時間を過ごせましたか？

はい、、、。

どうしたんですか？

すみません。夏休みがかなりきつくて。

大丈夫ですか？しっかり乗り切れたんだからgood jobですよ！達成感とか感じませんか？

多少は感じますけど、計画通りいかなかったし辛さの方が大きいですね。

そうなんですね。そんなあなたにはこの言葉を贈ります。

琴の弦は、張り過ぎると切れてしまう。しかし、緩過ぎては綺麗な音は出ない。適度な状態が一番良いのですよ。

ブッタ

 

自分を捨て、過酷な修行に没頭する若い修行僧にブッダが言ったとされる言葉。

その修行僧は琴の名手で、もう一度あの美しい音色を聞かせてほしいと頼むも、

「修行があるので琴を弾いている暇はありません」

と答える修行僧に対してブッダが諭した言葉。

頑張りすぎると自分を失ってしまう、ゆとりを持ちすぎれば何も生み出すことはできない。

心にゆとりを持てる状態が一番いい仕事やいい人間関係を持てるのかもしれません。

自分のやってきたことを悲観しすぎないように。

深刻にならず真剣に。

さらにもう一つ。

失望は一つの誘惑でもある。もう疲れた、止めた、降参だ、といって投げやりになれるという誘惑だ。

フランチェスコ・アルベローニ（イタリアの社会学者）

人は、努力しても報われなかったとき。

もしくは、何かに失望してしまったとき。

それに打ちひしがれてそこに倒れてしまいます。

しかし、本当に大事なことは、どんなに傷ついて躓いても、

立ち上がって再び目標に立ち向かうことなのかもしれません。

失望という誘惑に負けないようにしましょう（難しいけどね）

 

次はMaXさん。

MaXさんも３年生でしたね。MaXさんはずいぶん楽しそうというかやる気MaX！って感じですね。

そうですかー？（笑）

はい。夏休み期間上手くいったんですか？

もうバッチリです✨

それはすごい！達成感ありますよね。

はい！

そんな今勢いのあるあなたにはこの言葉を贈ります。

希望を持たない人は失望することもない。

ジョージ・バーナード・ショー（アイルランドの文学者、政治家, 1856-1950）

 

失望した時のショックはとても大きいです。

こんなことなら初めから期待しなければよかったと思いがちです。

しかし、希望がないと前向きに頑張る気力は沸きません。

たとえ失望しなくても、物事を成し遂げられなければ意味がありません。

しっかりと前を向いて生きることが必要なのかもしれません。

希望を持つあなたはいつか打ちひしがれることがあるかもしれません。しかし、それはもつ者の宿命だと思って乗り切って下さい。

 

 

最後は楽観さん。

楽観さんは高校２年生でしたよね？夏休みは十分な勉強時間を確保できましたか？

まあまあです。

１日どれぐらいの時間勉強に使ったのですか？

３時間ぐらいですかねー

宿題など含めてですか？

そうですねー。

受験生は１日１０時間以上やってる人もいますよ？

はい、知ってます。でも正直今はモチベ上がらなくて、高３になってから本気出せばいいかなーって。

 

分かりますよ。何かきっかけさえあれば今すぐにでもやりたい気持ちはあるんですよね？でも急に始めるのが何となく気恥ずかしい。

でも、そんなこと言ってるうちにすぐ高３になっちゃいますよ。

大学受験は低学年の時にどれだけ基礎が定着しているかでEasy modeかHard modeか決まるんですよ！

そんなあなたにこの言葉を送ります。

私は楽観主義者です。 しかしレインコートを持つ楽観主義者です。

ジェームズ・ハロルド・ウィルソン（英国の政治家1916–1995）

 

悲観的すぎると、前に進むことが怖くなってしまいます。

一方、楽観的な人は、躊躇なく前に進む行動をとります。

しかし、楽観的なことと、何の準備をしないこととは別です。

リスクを悲観的にとらえ、その対処をしたうえで、前に進むことが、成功への近道です。

最後まで今のような楽な気持ちで受験生活が過ごせるよう、今のうちに論理的な計画を立て、そして実行継続していきましょう。

 

誰もがこの3人と同じという訳では無いのは分かっています。状況、性格もろもろが人それぞれです。なので、自分の心に響く、刺さる言葉を探してみてはいかがですか？

担任助手1年齋藤蒼太