ブログプレイバックWEEK!! 2020年 9月 21日【力学】２質点系の運動その１ | 東進ハイスクール青葉台校大学受験の予備校・塾

ブログ

2021年 4月 9日　ブログプレイバックWEEK!! 2020年 9月 21日　【力学】２質点系の運動その１

4日目は中村さん！！

これは皆さんが衝撃を受けたブログではないでしょうか笑

残念ながら私文の私には何を言っているのか正直分かりませんが、

彼のすごさを伝えるためにご紹介いたします?

皆さんこんにちは。

横浜国立大学理工学部，担任助手1年の中村祐貴です。

皆さん進捗いかがですか？

最近は過去問演習や単元ジャンル別演習にいそしんでいることと思いますが，
最近ある生徒の答案を見て少し気になったので今回このテーマを扱います。
（皆さんが出している答案は私が受け取った時は軽く見させていただいてます笑）

今回の内容は全員が必ず押さえなければならない”must”の内容ですが，
続編（その２）はやや発展的な内容とはいえ，
知っていると物理的内容の見通しが良くなると思われるので，頑張っていきましょう。
（ただ難関大や物理系に進もうと考えている人にとっては続編も含めshould ~ mustです！）

今回の設定は以下の通りです。
とはいっても，非常に典型的なお話ですが。

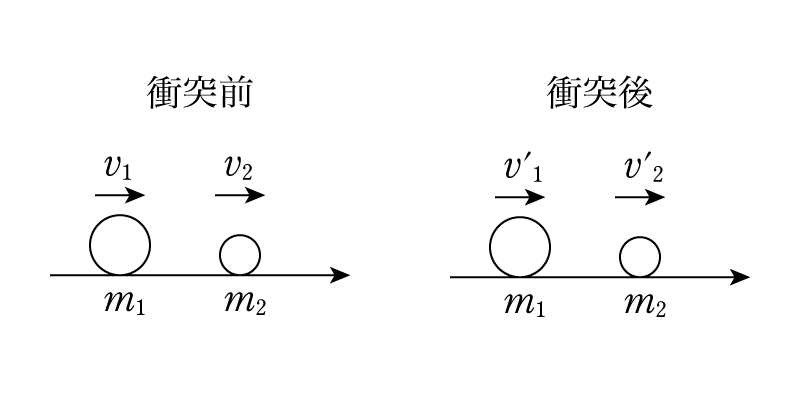
質量m_1,m₂の２質点が右向きを正とした速度v_1,v₂で弾性衝突し，
その直後のそれぞれの速度v_1^‘,v_2^‘を求めていきましょう。

画像引用：https://physics-school.com/two-body-energy/

問題自体は具体的な値であれば共通試験レベルなので，
できてほしいのですが，いかがでしょうか。

もし，手詰まりになったとするならば次のようにやったのではないでしょうか。

想定解答①

内力のみがはたらくので，運動量保存則より，
$\begin{eqnarray*} m_1v_1+m_2v_2=m_1v_1'+m_2v_2' \cdot\cdot\cdot(1) \end{eqnarray*}$

また，力学的エネルギー保存則より，
$\begin{eqnarray*} \frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1{v_1'}^2+\frac{1}{2}m_2{v_2'}^2 \cdot\cdot\cdot(2) \end{eqnarray*}$

え？これを代入するのかって？

まあこの式を立ててしまったのなら，解くためには代入するしかないでしょうか…
一応その過程を以下に示します。

代入計算過程

(１)式をv_2^‘について解いて，

$\begin{eqnarray*} v_2'=\frac{m_1}{m_2}(v_1-v_1')+v_2\cdot\cdot\cdot(1)' \end{eqnarray*}$
これを(２)式に代入して両辺を２倍すると，
（v_2^‘を消去してv_1^‘についての解を得たい！）
$\begin{eqnarray*} m_1v_1^2+m_2v_2^2=m_1{v_1'}^2+m_2\left(\frac{m_1}{m_2}(v_1-v_1')+v_2\right)^2 \end{eqnarray*}$
$\begin{eqnarray*} m_1v_1^2+\textcolor[rgb]{0.2,0.4,1}{m_2v_1^2}=m_1{v_1'}^2+\frac{m_1^2}{m_2}(v_1-v_1')^2+2m_1(v_1-v_1')v_2+\textcolor[rgb]{0.2,0.4,1}{m_2v_1^2} \end{eqnarray*}$
（消えること自体は展開前から見えていてほしいが）
青い部分を両辺から引いて整理すると
$\begin{eqnarray*} m_1v_1^2=m_1{v_1'}^2+\frac{m_1^2}{m_2}(v_1-v_1')^2+2m_1(v_1-v_1')v_2 \end{eqnarray*}$
となり，両辺をm₁で割って，
$\begin{eqnarray*} v_1^2={v_1'}^2+\frac{m_1}{m_2}(v_1-v_1')^2+2(v_1-v_1')v_2 \end{eqnarray*}$
をv_1^‘の２次方程式として整理すると，
$\begin{eqnarray*} \left(1+\frac{m_1}{m_2}\right){v_1'}^2-2\left(\frac{m_1}{m_2}v_1+v_2\right)v_1'+2v_1v_2-\left(1-\frac{m_1}{m_2}\right)v_1^2=0 \end{eqnarray*}$
$\begin{eqnarray*} v_1'=\frac{\frac{m_1}{m_2}v_1+v_2\pm\sqrt{\left(\frac{m_1}{m_2}v_1+v_2\right)^2-\left(1+\frac{m_1}{m_2}\right)\left(2v_1v_2-\left(1-\frac{m_1}{m_2}\right)v_1^2\right)}}{1+\frac{m_1}{m_2}} \end{eqnarray*}$
を得て，根号（ルート）の中身について項ごとに整理すると，
$\begin{eqnarray*} &\ &\left(\frac{m_1}{m_2}v_1+v_2\right)^2-\textcolor[rgb]{0.2,0.4,1}{\left(1+\frac{m_1}{m_2}\right)}\left(2v_1v_2-\textcolor[rgb]{0.2,0.4,1}{\left(1-\frac{m_1}{m_2}\right)}v_1^2\right)\\ &=&\left(\frac{m_1}{m_2}v_1\right)^2+2\frac{m_1}{m_2}v_1v_2+v_2^2+\left(\textcolor[rgb]{0.2,0.4,1}{1-\left(\frac{m_1}{m_2}\right)^2}\right)v_1^2-2\left(1+\frac{m_1}{m_2}\right)v_1v_2\\ &=&v_1^2-2v_1v_2+v_2^2\\ &=&(v_1-v_2)^2 \end{eqnarray*}$ となるから，
$\begin{eqnarray*} v_1'=\frac{\frac{m_1}{m_2}v_1+v_2\pm(v_1-v_2)}{1+\frac{m_1}{m_2}} \end{eqnarray*}$
を得る。
ここで，この複号の+側はv_1^‘=v₁という衝突直前の自明な関係が得られるだけなので，
－側を取ることで，求めるv₁‘の解
$\begin{eqnarray*} v_1'&=& \frac{\frac{m_1}{m_2}v_1+v_2-(v_1-v_2)}{1+\frac{m_1}{m_2}}\\ &=& \frac{\frac{m_1}{m_2}-1}{\frac{m_1}{m_2}+1}v_1+\frac{2}{\frac{m_1}{m_2}+1}v_2\\ &=& \frac{m_1-m_2}{m_1+m_2}v_1+\frac{2m_2}{m_1+m_2}v_2\\ \end{eqnarray*}$
を得る。これを(１)’式に代入してv₂‘の解
$\begin{eqnarray*} v_2'&=&\frac{m_1}{m_2}\left(v_1-\left(\frac{m_1-m_2}{m_1+m_2}v_1+\frac{2m_2}{m_1+m_2}v_2\right)\right)+v_2\\ &=&\frac{m_1}{m_2}\left(\frac{2m_2}{m_1+m_2}v_1-\frac{2m_2}{m_1+m_2}v_2\right)+v_2\\ &=&\frac{2m_1}{m_1+m_2}v_1+\frac{m_2-m_1}{m_1+m_2}v_2 \end{eqnarray*}$
を得る。

いやー，だるい！長い！

もちろんこの計算をこなす計算力は必要なので，
各自上の記述を隠してできるかどうか確認してみてほしいですが，
これを試験中にやるのは賢明ではないでしょう。

ではどうするのか。

実は，数学的な対称性を用いれば比較的容易に解くことができます。

想定解答①のつづき
(１)式及び(２)式は対称性に注意して次のように変形できる。
$\begin{eqnarray*} \left\{ \begin{array}{llll} m_1(v_1-v_1')&=&m_2(v_2'-v_2)&\cdot\cdot\cdot(1)''\\ \frac{1}{2}m_1(v_1^2-{v_1'}^2)&=&\frac{1}{2}m_2({v_2'}^2-v_2^2)&\cdot\cdot\cdot(2)' \end{array} \right. \end{eqnarray*}$
(１)”式の両辺は０でないので（０となるのは衝突前である！），
(２)’式を(１)”式で辺々割って両辺２倍することで，
$\begin{eqnarray*} v_1+v_1'=v_2+v_2' \end{eqnarray*}$
$\begin{eqnarray*} v_2'=v_1-v_2+v_1' \end{eqnarray*}$
となり，これと(１)’式とあわせて，
$\begin{eqnarray*} v_2'=v_1-v_2+v_1'&=&\frac{m_1}{m_2}(v_1-v_1')+v_2\\ \therefore \left(1+\frac{m_1}{m_2}\right)v_1'&=&\left(\frac{m_1}{m_2}-1\right)v_1+2v_2\\ \therefore v_1'&=&\frac{\left(\frac{m_1}{m_2}-1\right)v_1+2v_2}{1+\frac{m_1}{m_2}} \end{eqnarray*}$
（以下同様）

これならば計算量はさほど悪くはないですね。

一方，多くの「解けた」人は恐らく次のようにやったのではないでしょうか。

想定解答②
(２)式の代わりに弾性衝突であることから反発係数は１ゆえ，
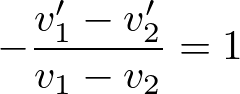
$\begin{eqnarray*} -\frac{v_1'-v_2'}{v_1-v_2}=1 \end{eqnarray*}$
を用いてこれを整理すると，
$\begin{eqnarray*} v_2'=v_1-v_2+v_1' \end{eqnarray*}$
（以下同様）

はい。こちらのほうが①より物理的な解答といえるでしょう。

ここまではこの記事を読んでくれた全員に抑えていただきたいmustの内容です。

しかし，これの「意味」がしっかりと分かっているならば，
より自然な解答を得ることができますが，

これを考えるのはみなさんの宿題とします。

続編で答え合わせをしましょう。

先に知りたい！という人は直接言ってくださればお答えします。

それでは，勉強頑張ってください。

担任助手１年　中村